Forecasting SEO
Felipe
Tabla de contenidos
TogglePara preparar las previsiones de crecimiento de distintos sitios webs y no hacerlo chupándose el dedo y poniéndolo al viento, lo mejor es crear un sistema de previsión mediante series temporales ( esto es cuando hablamos de una secuencia de valores observados a lo largo del tiempo y, por tanto, ordenados cronológicamente).
Visitas vs tiempo
Los objetivos del análisis de series temporales son diversos, pudiendo destacar la predicción, denominando predicción a la estimación de valores futuros de la variable en función del comportamiento pasado de la serie.
Evidentemente, aunque el valor futuro de una serie temporal no sea predecible con total exactitud, para que tenga interés el estudio el resultado tampoco puede ser completamente aleatorio, existiendo alguna regularidad en cuanto a su comportamiento en el tiempo, lo que hará posible su modelado y por ende, en su caso, la predicción.
Por lo tanto, si podemos encontrar patrones de regularidad en diferentes secciones de una serie temporal, podremos también describirlas mediante modelos basados en distribuciones de probabilidad.
El primer paso obligatorio para analizar una serie temporal es presentar un gráfico de la evolución de la variable a lo largo del tiempo:
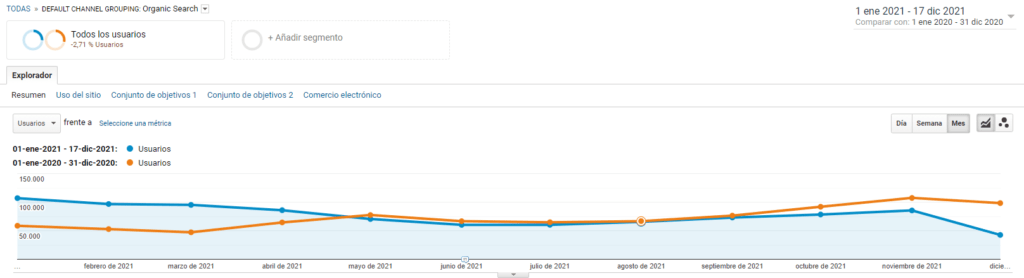
El siguiente paso consiste en determinar si la secuencia de valores es completamente aleatoria o si, por el contrario, se puede encontrar algún patrón a lo largo del tiempo, pues sólo en este caso podremos seguir con el análisis.
La metodología tradicional para el estudio de series temporales es bastante sencilla de comprender, y fundamentalmente se basa en descomponer las series en varias partes: tendencia, variación estacional o periódica, y otras fluctuaciones irregulares.
- Tendencia. Es la dirección general de la variable en el periodo de observación, es decir el cambio a largo plazo de la media de la serie.
- Estacionalidad. Corresponde a fluctuaciones periódicas de la variable, en periodos relativamente cortos de tiempo.
- Otras fluctuaciones irregulares. Después de extraer de la serie la tendencia y variaciones cíclicas, nos quedará una serie de valores residuales, que pueden ser o no totalmente aleatorios.
Cuando observemos la gráfica tendremos que extraer una tendencia y ver si existen periodos de estacionalidad que se puedan detectar fácilmente mediante periodos de tiempo mensual en comparación con años pasados.
Ahora bien: para eliminar esas otras fluctuaciones irregulares y detectar la tendencia de la gráfica utilizaremos filtros. Un filtro no es más que una función matemática que aplicada a los valores de la serie produce una nueva serie con unas características determinada.
Para esto utilizaremos un filtro de suavizado exponencial donde los últimos datos del periodo utilizado tienen más peso que los del total del resto del periodo, consiguiendo además así suavizar las fluctuaciones de plazos cortos y resaltar las tendencias o ciclos de plazos largo atenuando las desventajas de otros métodos como promedios móviles simples, en donde los datos para calcular el promedio tienen la misma ponderación.
Presentamos la ecuación de suavizado exponencial
Ft+1 = αYt + (1 – α)Ft (2)
Donde:
Ft+1 = Pronóstico de la serie de tiempo para el periodo de t + 1.
Yt = Valor real del periodo anterior al año a pronosticar. (que en nuestro caso serán cantidad de visitas del año anterior)
Ft = Valor real del periodo anteanterior al año a pronosticar. ( que en nuestro caso serán cantidad de visitas de hace 2 años )
α = Constante de suavización (0 ≤ α ≤ 1).
Constante de suavización
La elección de la constante de suavización α es crucial en la estimación de pronósticos futuros. Si la serie de tiempo contiene una variabilidad aleatoria sustancial, se preferirá un valor pequeño como constante de suavización. La razón de esta aseveración es que gran parte del error del pronóstico es provocado por la variabilidad aleatoria, por lo que un valor pequeño de α permite un pronóstico mejor.
Por el contrario, para una serie de tiempo con una variabilidad aleatoria relativamente pequeña, valores más elevados de la constante de suavización tienen la ventaja de ajustar con rapidez los pronósticos cuando ocurren errores de pronóstico y permitiendo, por lo tanto, que el pronóstico reaccione con mayor rapidez a las condiciones cambiantes.
En la práctica, el valor de α está entre 0,1 y 0,9
En nuestro caso cogeremos una constante de suavización alta que será 0,8 ya que nuestra serie de valores respecto a la gráfica presentada no establece una variabilidad aleatoria alta distinguiéndose claramente tendencias y estacionalidades en la gráfica.
Debemos de utilizar constantes de suavización más pequeñas si nuestros periodos de tiempo son más reducidos ya que la aleatoriedad sustancial será mucho más alta al no poder establecer correlaciones con largos periodos de tiempos anteriores.
Por tanto nuestra ecuación quedaría
- Ft+1 = αYt + (1 – α)Ft (2)
- Ft+1 = 0,8 · 899.744 + (1 – 0,8) · 809.615
- Ft+1 = 881.718
Una vez vayamos ajustando nuestro constante de suavización y valor real dentro de un periodo de tiempo con los resultados que hemos estimados y los que finalmente hemos conseguido podremos llegar a realizar predicciones más acertadas.
Si – por ejemplo – utilizáramos un valor real dentro de un periodo de tiempo más reducido ajustado al medio en que nos movemos como es Internet obtendremos resultados distintos pero que tendrán un mayor nivel de aleatoriedad sustancial.
Ft+1 = Pronóstico de la serie de tiempo para el periodo de t + 1.
Yt = Valor real del semestre anterior a pronosticar.
Ft = Valor real del periodo anteanterior al semestre a pronosticar.
α = Constante de suavización (0 ≤ α ≤ 1).
Ft+1 = αYt + (1 – α)Ft (2)
Ft+1 = 0,7 · 402.709 + (1 – 0,7) · 473.409
Ft+1 = 423.918
Variamos así el resultado de la anterior predicción siendo el valor real dentro del periodo de tiempo más reducido pero ajustándose al mismo tiempo con una constante de suavización menor que nos proporciona al mismo tiempo una aleatoriedad sustancial mayor.
Por lo que reduciendo el valor real dentro del periodo tiempo y la constante de suavización obtenemos una desviación en cantidad de visitas de un 3,8% presuponiendo que ha menor valor real dentro de un periodo de tiempo mayor % de desviación respecto a valores reales dentro de períodos más largos hasta que se consiga una constante de suavización ajustada que no proporcione desviaciones.
Tabla de contenidos
Toggle